Digital Elevation Models (DEMs) are required for a number of applications such as the orthorectification of satellite imagery, geoid computations, hydrological, environmental, and climate modelling.
Research is undertaken at the School of Surveying to create and assess DEMs. This led to the release of NZSoSDEM, a free 15m nationwide DEM.
Honours student Joshua Columbus later assessed the fractal nature of the Mt Cook region and the potential of using the fractal characteristic of terrain in the interpolation process.
 NZSoSDEM v1
NZSoSDEM v1
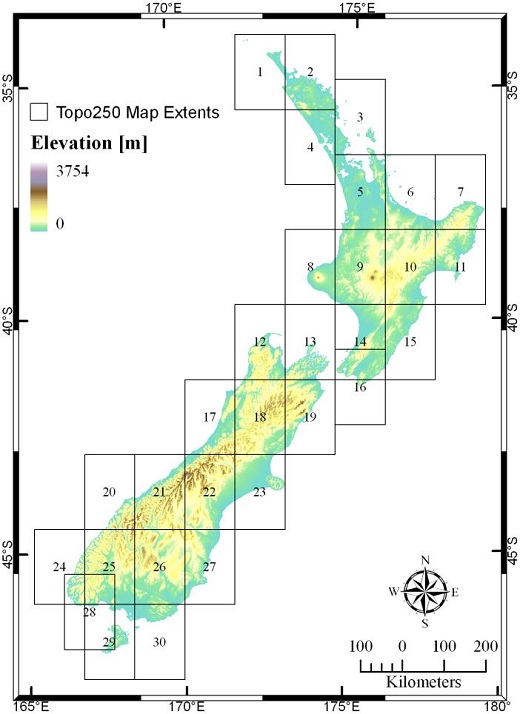
NZSoSDEM v1.0 is a free Digital Elevation Model (DEM) covering the whole of New Zealand at a spatial resolution of 15m, created by the School of Surveying by interpolating LINZ topographic vector data.
The DEM was created as a series of 30 maps which extent correspond exactly with the LINZ Topo250 topographic map series. Smaller regions can thus be obtained individually but also fit together seamlessly to create a full countrywide DEM.
The accuracy of this product was comprehensively assessed using a statistically sound selection of 3791 check points throughout the country. The comparison of results with other available country-wide DEM demonstrates an improvement of NZDEM_SoS_v1.0 in terms of quality that comes in addition with a finer spatial resolution (Columbus et al., 2011).
Fractal interpolation
Natural terrain has the ability to be characterised through fractal geometry as it displays self-similarities at different scales. In looking for ways to improve a DEMs representation of terrain, fractal based methods of interpolation have been tested to represent the fractal characteristics of terrain. To assess whether this fractal interpolation can significantly improve the representation of terrain compared to traditional interpolation techniques, a fractional Brownian motion interpolation is compared with a spline interpolation for a DEM over different scales. The fractal features of terrain are firstly extracted by estimating the fractal dimension before incorporating this into a fractional Brownian motion to represent the fractal nature of the surface (Columbus, 2011).
The results indicated fractal interpolation cannot improve the representation of terrain quantitatively. The stochastic nature involved with representing the fractal nature of terrain seems to always be outperformed by the classical techniques that aim to minimise errors. Positively, fractal interpolation can provide a qualitative improvement to the terrains representation. This is well suited for computer graphics applications and the creation of synthetic landscapes.
Resources and links
The NZSoSDEM is available at http://data.govt.nz/search/SearchForm?Search=nzsosdem&action_doCustomSearch=&x=0&y=0
and can be obtained freely from koordinates.com.